Coding Memo
[Codeforces] #448C Painting Fence 본문
Painting Fence
https://codeforces.com/problemset/problem/448/C
Problem - 448C - Codeforces
codeforces.com
Problem
Bizon the Champion isn't just attentive, he also is very hardworking.
Bizon the Champion decided to paint his old fence his favorite color, orange. The fence is represented as n vertical planks, put in a row. Adjacent planks have no gap between them. The planks are numbered from the left to the right starting from one, the i-th plank has the width of 1 meter and the height of ai meters.
Bizon the Champion bought a brush in the shop, the brush's width is 1 meter. He can make vertical and horizontal strokes with the brush. During a stroke the brush's full surface must touch the fence at all the time (see the samples for the better understanding). What minimum number of strokes should Bizon the Champion do to fully paint the fence? Note that you are allowed to paint the same area of the fence multiple times.
Input
The first line contains integer n (1 ≤ n ≤ 5000) — the number of fence planks. The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109).
Output
| Print a single integer — the minimum number of strokes needed to paint the whole fence. |
Examples
| Input |
| 5 2 2 1 2 1 |
| Output |
| 3 |
| Input |
| 2 2 2 |
| Output |
| 2 |
| Input |
| 1 5 |
| Output |
| 1 |
문제 해석
울타리를 세우고 페인트를 칠했을 때 스토로크를 사용하는 횟수의 최솟값를 구하는 문제이다.
페인트 칠은 가로 또는 세로로만 할 수 있다.
스트로크의 너비는 1이고 한번 칠하면 다시는 사용할 수 없다.
ex)
input
6
5 6 4 3 4 5
| input | output = 6 |
 |
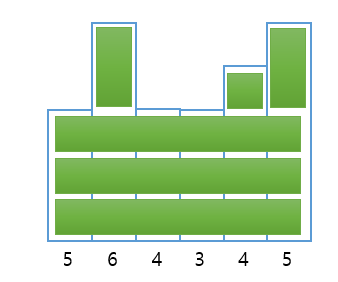 |
이 예시 같은 경우에는 받드시 위의 이미지 처럼 칠해야하는 것은 아니다. 다른 방법으로 칠해도 최솟값이 6이 나온다.
풀이
처음에는 백준에서 풀었던 #14719 빗물 문제랑 거의 비슷하다고 생각했지만 아니었다.
가로로만 탐색해서 풀려고 하니 가로로만 페인트칠을 했을 때 보다 세로로 칠했을 때의 횟수가 더 적게 나오는 경우가 있었다. (예 - 높이가 5인 울타리가 하나만 있을 때)
분할 정복으로 풀 수 있었다. (상당히 생각해내기가 어려웠다. 강의가 아니었으면 푸는 데 한참 걸렸을 수도 있다.)
울타리를 분할 시켜서 최솟값을 찾으면 된다.
단, 바로 위에서 언급했듯이 세로로만 칠했을 경우가 가로로 칠했을 경우보다 횟수가 적게 나오는 경우가 있다는 것에 유의하자.
예를 들어 아래 울타리가 있다고 해보자.

먼저 간단하게 생각하자.
가로로 가장 길게 칠하는 것이 페인트 스트로크가 덜 필요할 것이다.
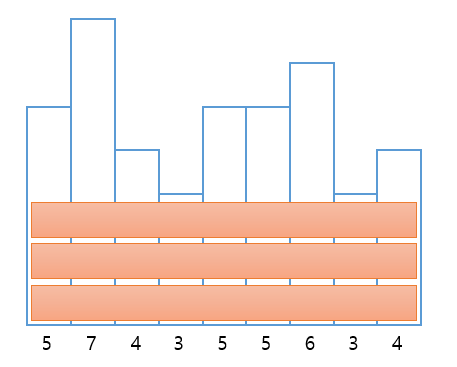
이 부분에 대해서는 n이 작을 경우 세로로 칠하는 것이 더 유리 할 수 있지만 이부분은 전부 칠하고 나서의 횟수와 세로로만 칠했을 때의 횟수(n)값과 비교해서 작은 값이 정답이므로 나중에 생각하기로 하자.
따라서 일단 위의 이미지와 같이 칠했을 경우 가장 유리한건 확실하다! (n개의 울타리 중 최솟값 높이인 3으로 3번 칠했다는 것을 기억하자)
이제 이 부분을 빼고 생각해보자

어떻게 해야 저부분을 가장 적은 스트로크로 칠 할 수 있을 것인가?
가로로만 길게길게 칠하는 것은 안된다.
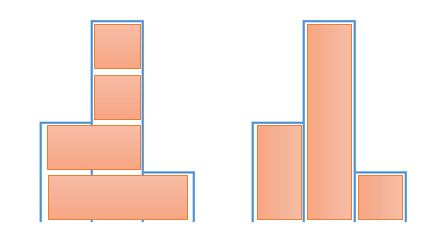
사실 이 이미지에 답이 나와있다. 남은 울타리들을 다시 하나의 문제에 주어진 울타리라고 생각하면 된다.
위에서 했던 것과 똑같이 가로로 먼저 길게 칠하고 나머지 부분을 또 다시 새로운 울타리라고 생각하고 풀면 된다.
(재귀 함수 이용)

최대한 작은 울타리로 나눈 다음 그 울타리에 대한 최솟값을 다시 울타리를 합쳐가면서 더하면 된다.
여기서 아까 말했던 세로로만 칠했을 때의 값과 비교하여 최솟값을 반환하면 된다.
-> min(울타리의 개수, paint 수)
| // 인자로 받은 울타리에 대해 페인트 칠 최소횟수 반환 함수 int solve (fences): int strokes = 0; int min = fences 중 가장 높이가 낮은 울타리 높이; strokes += min // 페인트 칠 횟수 더하기 do : fences 모두를 min 만큼 높이 줄이기 while (나누어진 울타리 덩어리가 없을 때까지): do : strokes = solve(나누어진 울타리) return min(strokes, fences 개수) // 세로로만 칠했을 때와 비교하여 작은 값 반환 |
fences는 배열로 하면 될 것이다.
사용 언어에 따라 다르겠지만, 배열에 대해서 어디서 어디까지가 이번에 확인할 울타리 덩어리들인지 바운더리를 정할 인자가 더 필요할 수 있을 것이다.
전체 코드
#include <iostream>
#define MAX 2147483647
using namespace std;
int A[5000];
int paint(int fences[], int size) {
int mn, strokes=0, s, e;
mn = MAX;
// 인자로 받은 fences에 대해 최대 길이(size)로 가로로 페이트를 몇 번 칠할 수 있는지
for (int i=0; i<size; i++) {
mn = min(mn, fences[i]);
}
// 인자로 받은 fence 높이 낮추기
for (int i=0; i<size; i++) {
fences[i] -= mn;
}
// 가로로 칠한 횟수 strokes에 누적
strokes += mn;
// 나머지 부분에 대해 solve 다시 호출해서 최솟값 찾기
s = 0; // 분할 할 때 배열 사이즈를 정하기 위한 수
while (s < size) {
while (s < size && fences[s] == 0) {
s++;
}
if (s==size) break; // 범위 벗어남 -> 뒤에 더이상의 fences 덩어리가 없을 경우
e = s+1; // 다음 포인터를 s+1 로 둠
// fences 가 이어져 있는 부분까지 확인
while (e < size && fences[e] > 0) {
e++;
}
strokes += paint(fences+s, e-s);
}
// 세로로만 칠했을 때(size)와 가로로 칠하고 나머지 부분 분할 정복했을 때와 비교하여 최솟값 반환
return min(size, strokes);
}
int main() {
cin.tie(NULL);
cout.tie(NULL);
ios_base::sync_with_stdio(false);
int n;
int t = 0;
cin >> n;
for (int i=0; i<n; i++) {
cin >> A[i];
}
cout << paint(A, n) << '\n';
return 0;
}
이 글은 '알고리즘 연습' 강의를 듣고 작성한 것임을 밝힙니다.
